Selamat malem guys, gue mau ngeshare lagi nih soal-soal tentang fisika, buat elo nih yang ngakunya "Cinta Fisika" Lo harus baca ini dan coba dipahami. Mudah-mudah jadi refernsi buat belajar lo nih. Oke soal disini gw ambil dari buku Analytical Mechanics Penulisnya Fowles dan Cassiday. Menurut gw soal ini keren, kenapa?? karena soal yang gue ambil adalah soal yang GAK ADA ANGKA sama sekali, tapi jawabannya panjang banget, makanya seru buat diselesaikan. Oke langsung aja ke soal dan pembahasan !
1. Sebuah benda mengalami gerak jatuh bebas. Tentukakanlah persamaa Lagrangiannya, momentum umumnya, gaya umumnya dan persamaan geraknya !
c. Gaya umumnya :
d. Persamaan geraknya :
2. Sebuah benda mengalami gerak peluru. Tentukan Persamaan Lagrangiannya, momentum umumnya, gaya umumnya dan Persamaan geraknya !
Penyelesaian :
Sebelum kita menyelesaikan soal di atas, mari kita tentukan terlebih dahulu koordinat yang ingin kitagunakan. Koordinat tersebut kita gambarkan sebagi berikut
Sehingga dapat ditentukan :
1. Sebuah benda mengalami gerak jatuh bebas. Tentukakanlah persamaa Lagrangiannya, momentum umumnya, gaya umumnya dan persamaan geraknya !
Penyelesaian :
Sebelum
kita menyelesaikan soal di atas, kita gambarkan dulu terlebih dahulu koordinat
yang ingin kita gunakan. Gambar di bawah ini adalah gambaran umum dari beda
yang mengalami jatuh bebas.
Dari
gambar di atas mari kita tentukan constrain terlebih dahulu pada sistem di
atas. Constrain yang terdapat pada sistem tersebut adalah arah sumbu x dan arah
sumbu z yaitu yang besarnya sama dengan nol.
Dan sistem tersebut hanya memiliki satu derajat
kebebasan yaitu x. Mari kita tentukan :
a. Persamaan Lagrangenya :
Dari sistem di atas
diperoleh energy kinetic benda yaitu :
Untuk
energy potensialnya adalah :
Maka
persamaan Lagrangiannya adalah :
b. Momentum umumnya :
d. Persamaan geraknya :
2. Sebuah benda mengalami gerak peluru. Tentukan Persamaan Lagrangiannya, momentum umumnya, gaya umumnya dan Persamaan geraknya !
Penyelesaian :
Sebelum kita menyelesaikan soal di atas, mari kita tentukan terlebih dahulu koordinat yang ingin kitagunakan. Koordinat tersebut kita gambarkan sebagi berikut
Dari gambar di atas, constrain yang
diberikan sistem hanya satu yaitu sumbu z = 0. Derajat kebebasan pada sistem
tersebut adalah sumbu x dan y. Sehingga dapat kita tentukan energy kinetic dan
energy potensial sistem yaitu :
(catatan : Pada sumbu x benda tidak
memiliki energy potensial)
a. Persamaan
Lagrangiannya :
b. Momentum
umumnya :
c. Gaya umumnya :
d. Persamaan Geraknya :
3. Carilah
persamaan Hamilton canomic untuk kasus :
a.
Pendulum Sederhana
b.
Pesawat Atwood
Penyelesaian :
a.
Pendulum Sederhana
Gerak pada pendulum dapat digambarkan sebagai
berikut
Untuk
menyelesaikan persamaan Hamiltonian dari sistem di atas, terlebih dahulu kita
cari persamaan Lagrange nya. Persamaan Lagrange tersebut adalah :
Energi
kinetic pada sistem dapat diperoleh dengan melihat gambar di atas. Dari gambar
di atas kita peroleh bahwa :
Sehingga :
Untuk
energy Potensialnya adalah :
Setelah
itu dimasukkan ke dalam persamaan, menjadi :
Karena
pada mekanika Hamiltonian harus terdapat komponen momentumnya, maka untuk memperoleh
komponen tersebut kita turunkan persamaan berikut.
Sehingga
diperoleh persamaan Hamiltoniannya menjadi
Menurut
persamaan gerak Hamilton canonic yaitu
Sehingga jika kita
subtitusi persamaan di atas, diperoleh persamaan geraknya yaitu :
b.
Pesawat Atwood
Sistem pada pesawat
Atwood dapat dilihat pada gambar dibawah ini
Untuk
memperoleh persamaan Hamiltonian, terlebih dahulu kita tentukan dulu persamaan
Lagrangenya. Untuk memperoleh persamaan Lagrangenya kita tentukan dulu
constrain yang ada pada sistem tersebut. Constrain yang terdapat pada sistem
tersebut ada 5, yaitu : 4 di antaranya adalah arah sumbu x dan z pada m1 dan m2
yang mana pada sumbu tersebut bernilai nol. Contrain yang selanjutnya adalah
panjang tali menghubungkan kedua beban tersebut. Sehingga bisa kita list
constrain tersebut sebagai berikut.
Derajat
kebebasan pada sistem ini hanya satu yaitu sumbu y. Sehingga diperoleh
energy kinetic dan energy potensial sebagai berikut.
Sehingga
persamaan Lagrangiannya adalah
Karena
untuk memperoleh persamaan Hamiltonian kita membutuhkan komponen momentumnya,
maka Persamaan Lagrange di atas kita ubah hitung dengan persamaan :
Setelah
itu diperoleh persamaan Hamiltoniannya sebagai berikut.
Maka
persamaan gerak Hamilton canonicnya yaitu :
Jika kedua persamaan di atas disubtitusi maka diperoleh
persamaan gerak dari sistem tersebut yaitu :



















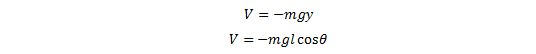













Comments
Post a Comment